Contoh Soal Pola Bilangan – Materi pola bilangan merupakan salah satu materi dasar dari baris dan deret. Sebagai materi dasar, tentunya ini harus dipahami agar materi lain mudah dipelajari.
Memahami dan mempelajari pola bilangan dalam matematika akan cukup efektif bila mempelajari contoh soal. Karena memang materi akan diterapkan untuk menjawab setiap soal.
Untuk membantu kalian mendalami materi pola bilangan, maka pada kesempatan kali ini inspired2write akan sajikan beberapa contoh soal pola bilangan beserta jawabannya.
Namun, sebelum mencoba mengerjakan latihan soal pola bilangan, maka ada baiknya kalian mempelajari kembali sekilas materi terkait pola bilangan di bawah ini terlebih dahulu.
Materi Pola Bilangan
Pola bilangan adalah susunan angka-angka yang membentuk pola tertentu, misalkan segitiga, garis lurus dan lainnya. Dalam matematika pola bilangan terbagi jadi beberapa jenis yaitu :
1. Pola Bilangan Persegi Panjang
Pola bilangan persegi panjang ialah pola dari bilangan-bilangan yang membentuk persegi panjang. Contohnya yaitu 2, 6, 12, 20, … sementara untuk rumusnya yakni Un = n(n+1).

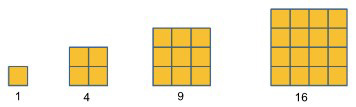
2. Pola Bilangan Persegi
Pola bilangan persegi adalah susunan bilangan yang dapat membentuk persegi oleh bilangan kuadrat, contohnya 1, 4, 9, 16, 25, 36. Pola bilangan persegi ini mengikuti rumus Un = n2
3. Pola Bilangan Garis Lurus
Sementara untuk pola bilangan garis kurus adalah susunan bilangan yang penulisannya mengikuti pola garis lurus. Adapun rumus menentukan pola bilangan garis lurus yakni Un = n

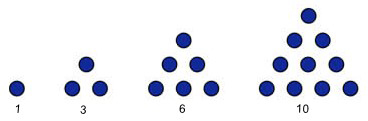
4. Pola Bilangan Segitiga
Pola bilangan segitiga yaitu suatu pola yang tersusun membentuk seperti segitiga yang tersusun dari beberapa bilangan, misalkan 3, 6, 10, 15 … dengan rumus Un = n(n+1)/2
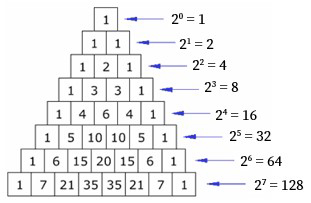
5. Pola Bilangan Segitiga Pascal
Pola segitiga pascal adalah pola dari jumlah bilangan pada baris segitiga pascal, misalnya baris ke-4 atau N4 terdiri dari 1, 2, 1. Barisan bilangannya 1, 2, 4, 8, 16 … Rumusnya : Un = 2n-1
6. Pola Bilangan Ganjil
Pola bilangan ganjil ialah barisan bilangan yang mana pola bilangannya terdiri dari bilangan ganjil, contohnya 1, 3, 5, 7, 9, 11… Rumus menentukan pola bilangan ganjil : Un = 2n-1.
7. Pola Bilangan Genap
Pola bilangan genap merupakan pola barisan, dimana bilangannya adalah kumpulan bilangan genap, misalnya 2, 4, 6, 8, 10, 12, … Rumus menentukan pola bilangan genap yakni Un = 2n.
Contoh Soal Pola Bilangan

Setelah mempelajari dan memahami materi pola bilangan, selanjutnya kalian bisa memahami contoh soal beserta jawabannya di bawah ini sebelum mencoba latihan soal pola bilangan.
A. Contoh Soal Pola Bilangan Pilihan Ganda
Contoh Soal 1
Diketahui pola bilangan 4, 7, 10, 13,…,… maka angka pada pola ke-7 yaitu …
a. 22
b. 20
c. 17
d. 19
Jawabannya : a
Pembahasan :
⇒ Suku pertama (a) = 4
⇒ Beda (b) = 7-4 = 10-7 = 3
⇒ Ditanyakan suku ke-7 = U7
⇒ U7 = a + (n11)b = 4 (n-1)3 = 22
Contoh Soal 2
Diketahui barisan bilangan: 3, 8, 13, 18, 23, … Suku ke-32 adalah ….
a. 153
b. 168
c. 465
d. 158
Jawabannya : d
Pembahasan :
Sesuai soal di atas, diperoleh suku pertama yakni 3 (a=3) dan beda setiap sukunya 5 (b=5)
⇒ Un = a + (n – 1)b
⇒ U32 = a + 31b U32 = 3 + 31 × 5
⇒ U32 = 3 + 155 = 158
Contoh Soal 3
Pola bilangan untuk barisan 44,41,38,35,32,⋯44,41,38,35,32,⋯ memenuhi rumus…
a. Un=47−3n
b. Un=46−2n
c. Un=44−n
d. Un=3n+41
Jawabannya : a
Pembahasan :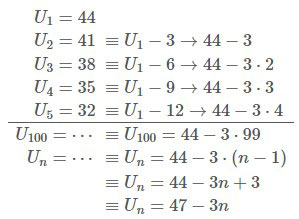
Contoh Soal 4
Diketahui barisan geometri 2, 10, 50, 250,… maka nilai U8 ialah …
a. 78.125
b. 156.000
c. 150.000
d. 56.750
Jawabannya : b
Pembahasan :
Untuk menentukan U8 terlebih dahulu mengetahui rasio (r) dari barisan tersebut. Nilai a barian tersebut = 2 dan r = 10/2 = 5, maka U8 adalah
⇒ Un = a × rn-1
⇒ U8 = 2 × 58-1
⇒ U8 = 156.000
Contoh Soal 5
2, 4, 3, 6, …, 10, 9, 18
a. 6
b. 8
c. 5
d. 7
Jawabannya : c
Pembahasan :
Untuk menemukan pola operasi aritmetik pada barisan bilangan diatas, harus digunakan metode coba-coba.
Dari pola di atas diperoleh bilangan 6 – 1 = 5
Contoh Soal 6
Jika suatu barisan 2,8,32,128,⋯ memenuhi rumus Un=2an+b maka nilai a×b=⋯
a. 1
b. 2
c. -2
d. -1
Jawabannya : c
Pembahasan :
Contoh Soal 7

Contoh Soal 8
Jika diketahui 4, 8, 18-x merupakan deret geometri. Maka nilai x adalah…
a. 6
b. 2
c. 3
d. 4
Jawaban : b
Pembahasan :
Contoh Soal 9
Jumlah 30 bilangan ganjil pertama yang dimulai dari 1 adalah….
a. 950
b. 900
c. 850
d. 800
Jawaban : b
Pembahasan :
Contoh Soal 10
Diketahui bilangan segitiga pascal, maka jumlah bilangan pada baris ke-6 adalah…
a. 21
b. 32
c. 43
d. 56
Jawaban : b
Pembahasan :
B. Contoh Soal Pola Bilangan Essay
Contoh Soal 1
Perhatikan pola bilangan berikut!
2, 100, 4, 95, 7, 90, 11, 85,…,…
Tentukan bilangan ke-9 dan ke-10 dari pola di atas!
Pembahasan :
Jika diperhatikan, sebenarnya terdapat dua buah pola bilangan yang diselang-seling.
⇒ 2, 4, 7, 11, ….
⇒ +2, +3, + 4, +5 dst
⇒ 100, 95, 90, 85,….
⇒ -5, -5, -5, -5, dst
⇒ Jadi, 2, 100, 4, 95, 7, 90, 11, 85, 16, 80
Contoh Soal 2
Diketahui barisan bilangan 4, 10, 16, 22, 28, … Tentukanlah suku ke-30
Pembahasan :
⇒ a = 4
⇒ b = 6
⇒ Un = a + (n-1)b
⇒ U30 = 4 + (30-1)6
⇒ U30 = 4 + 29 × 6
⇒ U30 = 4 + 174
⇒ U30 = 178
Contoh Soal 3
Diketahui suku ke-n suatu barisan dinyatakan dengan Un = 5n + 4. Berapakah hasil penjumlahan suku ke-12 dan ke-14
Pembahasan :
Un = 5n + 4
Suku U12 :
U12 = 5 × 12 + 4
U12 = 60 + 4
U12 = 64
Suku U14 :
U14 = 5 × 14 + 4
U14 = 70 + 4
U14 = 74
Jadi
U12 + U14 = 64 + 74 = 138
Contoh Soal 4
Jika diketahui 2 suku dari pola barisan ialah U23 = 77 dan U77 = 23. Suku ke berapakah pada barisan tersebut bernilai 0?
Pembahasan :
Un = a + (n-1)b
Ut = a + (t-1)b
U23 = a + (23-1)b
77 = a + 22b … (1)
U77 = a + (77-1)b
23 = a + 76b
a = 23 – 76b … (2)
Substitusikan (2) ke (1)
77 = a + 22b
77 = 23 – 76b + 22b
54b = 23 – 77 = -54
b = -1
Substitusikan nilai b ke (2)
a = 23 – 76b
a = 23 – 76 × (-1)
a = 23 + 76
a = 99
Substitusikan nilai a dan b ke Ut
Ut = a + (t-1)b
0 = 99 + (t-1)×(-1)
0 = 99 – t + 1
0 = 100 – t
t = 100
Jadi, suku bernilai 0 pada barisan diatas ialah suku ke 100 atau U100 = 0.
Contoh Soal 5
Diketahui jumlah n suku pertama sebuah deret aritmetika ialah 1.325. Dengan U3 = 13 dan U7 = 29. Maka nilai n adalah …
Pembahasan :
Download Contoh Soal Pola Bilangan
Untuk mencoba mengukur kemampuan serta mengetahui seberapa dalam materi pola bilangan yang kalian kuasai, silahkan download latihan soal di bawah ini untuk kalian coba kerjakan.
Nah, itulah contoh soal pola bilangan beserta jawabannya dari inspired2write.com. Pola bilangan sangat penting untuk dipelajari karena sering muncul dalam SOAL AKM SMP KELAS 8. Demikianlah contoh soal pola bilangan dari kami, semoga saja informasinya bermanfaat.