Contoh Soal Persamaan Lingkaran Kelas 11 – Buat kalian kelas 11 SMA, SMK atau sederajat, siapkah kalian mempelajari ilmu baru mapel matematika atau mungkin ingin memperdalam materi persamaan lingkaran? SUDAH SIAP!!!! perhatikan dengan seksama ulasan berikut ini.
Dalam materi pelajaran matematika kelas 11, kalian akan dihadapkan dengan kompetensi dasar untuk menentukan persamaan lingkaran. Dimana materi ini sangat penting untuk di pelajari karena kerap kali muncul dalam soal AKM kelas 11 numerasi dan ujian sekolah.
Persamaan lingkaran merupakan sebuah persamaan yang berhubungan dengan bangun lingkaran dan unsur-unsur didalamnya. Dalam soal-soal materi persamaan lingkaran tersebut biasanya terdapat hubungan antara titik pusat lingkaran dengan titik-titik tertentu.
Nah, agar memahami lebih dalam materi persamaan lingkaran kelas 11 SMA, SMK atau sederajat, maka kami siap membantu. Dimana kali ini kami, akan membantu kalian dengan menyajikan sejumlah contoh soal persamaan lingkaran yang dapat dipelajari di bawah ini.
Materi Rumus Persamaan Lingkaran Kelas 11
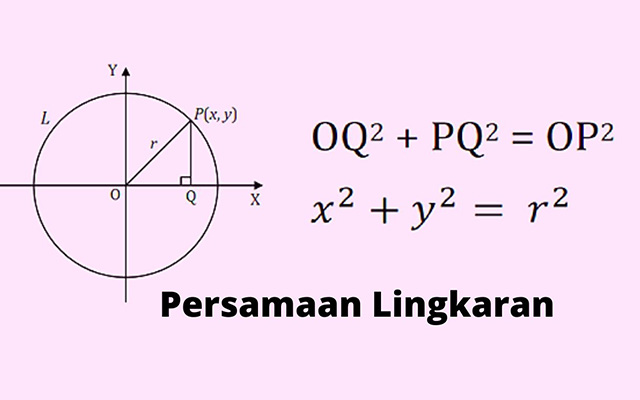
Ada dua aturan yang harus dipahami dari suatu bentuk persamaan lingkaran yaitu pusat (0,0) dan (a,b) dengan masing-masingnya berjari-jari r.
Apabila sebuah lingkaran memiliki pusat (0,0) dengan jari-jari r, maka bentuk persamaannya adalah x2 + y2 = r2.
Jika sebuah lingkaran berpusat pada (a,b) dengan jari-jari r, maka bentuk persamaannya adalah (x – a)2 + (y – b)2 =r2.
Lalu, apa bedanya bentuk persamaan di atas dengan x2 + y2 + Ax + By – C = 0 ? Sebenarnya sama saja, bedanya kalian diminta untuk mengkonversi bentuk standar ke bentuk umum.
Jadi, tetap menggunakan rumus persamaan lingkaran (x – a)2 + (y – b)2 =r2, lalu konversikan kedalam bentuk umum persamaan lingkaran yaitu x2 + y2 + Ax + By – C = 0. Hasilnya sama.
A. Persamaan Lingkaran

1. Menentukan titik pusat dan jari-jari.
2. Menentukan persamaan lingkaran sesuai x2 + y2 = r2 atau (x – a)2 + (y – b)2 =r2.
B. Persamaan Jarak pada Lingkaran
- Jarak titik (x1,y1) ke titik (x2,y2)
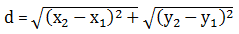
- Jarak titik (x1,y1) ke garis Ax + By + C = 0
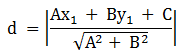
C. Persamaan Garis Singgung
Garis singgung ialah garis yang memotong lingkaran di satu titik. Ada tiga hal yang menentukan persamaan garis singgung, yaitu :
1. Apabila diketahui titik pada lingkaran
Ada titik (x1,y1) pada lingkaran, maka persamaannya harus diubah menjadi seperti berikut ini.

2. Apabila diketahui titik diluar lingkaran
- Tentukan persamaan garis kutub (poral) dari titik A(x1,y1) terhadap lingkaran.
- Melalui titik potong antara garis kutub lingkaran.
- Tentukan persamaan garis singgung melalui titik potong garis kutub.
3. Apabila diketahui gradien
Apabila telah diketahui titik (x1,y1) dengan gradien m pada lingkaran. Maka :

D. Kedudukan Dua Lingkaran
Jika jarang antara titik pusat lingkaran dituliskan d, serta r2 dan r2 adalah jari-jari pada masing-masing kedua lingkaran, maka kedua lingkaran tersebut akan saling :
- Saling lepas, sehingga d > r1 + r2
- Saling bersinggungan di dalam lingkaran, sehingga d = |r1 – r2|
- Saling bersinggungan di luar lingkaran, sehingga d = r1 + r2
- Saling berpotongan, sehingga |r1 – r2| < d < r1 + r2
- Lingkaran di dalam lingkaran, sehingga d = < r1 – r2
Contoh Soal Persamaan Lingkaran Kelas 11
Itulah sedikit uraian terkait persamaan lingkaran. Sampai disini sudahkan kalian paham dengan persamaan lingkaran! agar kalian semakin paham dengan persamaan lingkaran, maka sebaiknya kalian perhatikan beberapa contoh soal persamaan lingkaran kelas 11 berikut ini.
Contoh Soal I
| Sebuah lingkaran dengan pusat (1,2) memiliki jari-jari 5. Tentukan persamaan lingkaran tersebut! Jawab : p = (1,2) → pusat lingkaran (a,b) r = 5 Karena pusat lingkaran (a,b), maka rumus persamaan yang digunakan adalah (x – a)2 + (y – b)2 = r2. ⇒ (x – a)2 + (y – b)2 = r2 ⇒ (x – 1)2 + (y – 2)2 = 25 Berikutnya, konversikan bentuk standar ke dalam bentuk umumnya : ⇒ x2 – 2x + 1 + y2 – 4y + 4 = 25 ⇒ x2 + y2 – 2x – 4y – 20 = 0 Jadi, bentuk umum persamaan lingkaran pusat (2,3) dan jari-jari 5 adalah x2 + y2 – 2x – 4y – 20 = 0 |
Contoh Soal II
| Persamaan lingkaran yang melalui titik (3,-2) dan memiliki titik pusat (3,4) adalah …. Jawab : Diketahui titik (3,-2) dan pusat (3,4) Cari nilai r terlebih dahulu melalui rumus di bawah ini: (x – a)² + (y – b)² = r² (3 – 3)² + (-2 – 4)² = r² 0 + 36 = r² r = √36 r = 6 Jadi persamaan lingkaran tersebut adalah : (x – a)² + (y – b)² = r² (x – 3)² + (y – 4)² = 6² x² – 6x + 9 + y² – 8y + 16 = 36 x² + y² – 6x – 8y + 25 = 36 x² + y² – 6x – 8y – 11 = 0 |
Download Soal Persamaan Lingkaran Kelas 11 PDF
Nah, buat kalian yang ingin mencoba sendiri mempelajari dan mengasah hasil belajar setelah memperhatikan uraian materi dan contoh soal di atas, maka kalian bisa mencoba latihan soal persamaan lingkaran yang dapat kalian download secara gratis melalui tautan berikut.
Nah, itulah informasi lengkap yang dapat inspired2write.com sajikan buat kalian semua mengenai contoh soal persamaan lingkaran kelas 11 untuk jenjang SMS, SMK, MA atau sederajat lengkap dengan jawabannya. Demikianlah, semoga artikel di atas menambah wawasan kalian.