Contoh Soal Himpunan Kelas 7 – Mempelajari, memahami dan mencoba menjawab soal-soal terkait himpunan merupakan metode belajar yang terbilang efektif untuk siswa kelas 7.
Dengan mempelajari contoh-contoh soal himpunan, maka kalian bisa menerapkan setiap materi himpunan untuk menjawab setiap soal. Ini tentunya sangat efektif untuk diterapkan.
Nah, agar memudahkan kalian dalam belajar materi tentang himpunan dalam Matematika. Berikut ini inspired2write.com akan menyajikan informasi terkait contoh soal himpunan.
Bukan hanya itu saja, kami juga akan memberikan sekilas materi tentang himpunan. Adapun untuk penjelasan lebih lengkap lagi terkait himpunan, langsung saja simak ulasan di bawah ini.
Materi Himpunan Kelas 7

Sebelum mempelajari dan menjawab contoh soal himpunan, maka sebaiknya kalian pahami dan pelajari materi terkait himpunan dalam Matematika untuk siswa kelas 7 terlebih dahulu.
Dibawah ini akan kami sajikan pengertian, jenis, dan informasi lengkap terkait himpunan untuk kelas 7 SMP/MTs/Sederajat. Langsung saja simak ulasan selengkapnya di bawah ini.
A. Pengertian Himpunan
Himpunan adalah kumpulan benda atau objek yang dapat didefinisikan dengan jelas, sehingga dengan tepat dapat diketahui objek yang termasuk himpunan dan yang tidak termasuk dalam himpunan tersebut.
Contoh Himpunan :
- Himpunan hewan karnivora
- Kumpulan kabupaten yang ada di provinsi Yogyakarta
- Kumpulan nama siswa kelas 7 C yang diawali huruf R
B. Jenis-Jenis Himpunan
- Himpunan kosong
Himpunan kosong ialah himpunan yang tidak memiliki anggota. Contoh : Himpunan buah rasanya asin.
- Himpunan tak kosong
Himpunan tak kosong yaitu himpunan yang memiliki anggota. Contoh : Himpunan bulangan prima kurang dari 10.
C. Pengertian Himpunan Semesta
Himpunan semesta atau semesta pembicaraan adalah himpunan yang memuat semua anggota atau objek himpunan yang dibicarakan. Himpunan semesta biasanya dilambangkan dengan S.
Contoh Himpunan Semesta
Misalnya A = {2, 3, 5, 7}, maka himpunan semesta yang mungkin dari himpunan A adalah sebagai berikut ;
- S = {bilangan prima} atau
- S = {bilangan asli} atau
- S = {bilangan cacah}
Himpunan semesta dari {kerbau, sapi, kambing} adalah {binatang}, {binatang berkaki empat}, atau {binatang memamah biak}.
D. Pengertian Diagram Venn
Diagram Venn yaitu suatu cara menyatakan himpunan dengan menggunakan gambar. Diagram venn dapat diartikan sebagai diagram yang didalamnya terdapat seluruh kemungkinan benda ataupun objek.
Dalam diagram Venn, himpunan semesta dinyatakan dengan daerah persegi panjang. Sementara himpunan lain dalam himpunan semesta dinyatakan dengan kurva mulus tertutup sederhana dan noktah-noktah untuk menyatakan anggotanya.
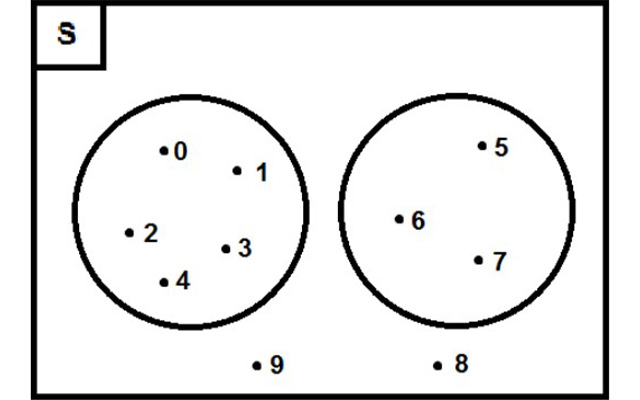
Contoh diagram venn
Diketahui :
S = {0, 1, 2, 3, 4, …, 9};
P = {0, 1, 2, 3, 4}; dan Q = {5, 6, 7}.
Himpunan S = {0, 1, 2, , 4, …, 9} adalah himpunan semesta. Dalam diagram venn, himpunan semesta dinotasikan dengan S berada di pojok kiri.
E. Notasi & Anggota Himpunan
Suatu himpunan biasanya dilambangkan dengan huruf besar A,B,C, …,Z. Adapun benda atau objek yang termasuk dalam himpunan tersebut ditulis dengan menggunakan pasangan kurung kurawal {…}.
Contoh :
- A adalah himpunan bilangan cacah kurang dari 6, sehingga A = {0,1,2,3,4,5}.
- P adalah himpunan huruf-huruf vokal, sehingga P = {a,i,u,e,o}.
F. Menyatakan Sesuatu Himpunan
Bisa dinyatakan dengan 3 cara :
I. Dengan kata-kata
Contoh:
- P adalah himpunan bilangan prima antara 10 dan 40. Ditulis
- P={bilangan prima antara 10 dan 40}.
II. Dengan notasi pembentuk himpunan
Contoh:
- P adalh himpunan biangan prima antar bilangan 10 dan 40.
- Ditulis P={10<x<40, x ∈ bilangan prima}.
III. Dengan mendaftar anggota-anggotanya
Contoh:
- P adalah himpunan bilangan prima antar 10 dan 40. Ditulis
- P= {11,13,17,19,23,29,31,37}
G. Himpunan Bagian
Himpunan A merupakan himpunan bagian B jika setiap anggota A menjadi anggota B
dengan menotasikan A⊂B atau B⊃A.
Himpunan A bukan merupakan himpunan bagian B jika terdapat anggota A yang
bukan anggota B dan dinotasikan A⊄B.
Setiap himpunan A merupakan himpunan bagian dari himpunan A sendiri, ditulis
A⊂A.
Contoh :
Diketahui K = {1,2,3}, tentukan himpunan bagian dari K yang mempunyai
- Satu anggota
- Dua anggota
- Tiga anggota
Dijawab :
- Himpunan bagian K yang mempunyai 1 anggota adalah {1},{2},{3}
- Himpunan bagian K yang mempunyai 2 anggota adalah {1,2},{1,3},{2,3}
- Himpunan bagian K yang mempunyai 3 anggota adalah {1,2,3}
H. Menentukan Banyaknya Himpunan Bagian dari Suatu Himpunan
Banyaknya himpunan bagian dari suatu himpunan adalah 2¬¬n, dengan n banyaknya anggota himpunan tersebut. Banyaknya himpunan bagian adalah himpunan kuasa.
Contoh:
- Himpunan bagian dari {a,b,c,d} yang mempunyai 0 anggota ada 1, yaitu { };
- 1 anggota ada 4, yaitu {a},{b},{c},{d};
- 2 anggota ada 6, yaitu {a,b},{a,c},{a,d},{b,c},{b,d},{c,d};
- 3 anggota da 4, yaitu {a,b,c},{a,b,d},{a,c,d},{b,c,d};
- 4 anggota ada 1, yaitu {a,b,c,d};
Contoh Soal Himpunan Kelas 7

Berikut ini adalah beberapa contoh soal himpunan kelas 7 SMP/MTs/Sederajat Kurikulum terbaru. Jadi bagi kalian siswa kelas 7, silahkan pelajari contoh soal di bawah ini untuk belajar.
Contoh Soal 1
| Survei membuktikan 30 anak menyukai serial Upin Ipin, 20 anak menyukai serial Shaun the Seep, dan 19 anak menyukai serial Upin Ipin dan Shaun the Seep. Banyaknya peserta yang mengikuti survei adalah …. anak. A. 30 B. 31 C. 32 D. 33 Pembahasan : Misal: – S = himpunan semesta – Uu = suka Upin Ipin – Ss = suka Shaun the Seep – Uu ∩ Ss = suka keduanya Diket: – n(Uu) = 30 anak – n(Ss) = 20 anak – n(Uu ∩ Ss) = 19 anak Dit: n(S)…? Jawab: n(S) = n(Uu) + n(Ss) – n(Uu ∩ Ss) n(S) = 30 + 20 – 19 n(S) = 31 Jawabannya : B |
Contoh Soal 2
| Diketahui A = {2, 3, 4} dan B = {1, 3}, maka A ∪ B adalah …. A. {3} B. {1, 2, 3, 4} C. {1, 3} D. {2, 4} Pembahasan : Diket: – A = {2, 3, 4} – B = {1, 3} Maka, A ∪ B = {1, 2, 3, 4} Jawabannya : B |
Contoh Soal 3
| Jika himpunan A B dengan n(A) = 11 dan n(B) = 18 maka n (A B ) = . . . A. 7 B. 11 C. 18 D. 28 Pembahasan : n ( A ) = 11 n ( B ) = 18 Setiap A B maka A ∩ B = A Sehingga n ( A ∩ B ) = n ( A ) n ( A ∩ B ) = 11 Jawabannya : B |
Contoh Soal 4
| Diberikan P = {1,2,3,9,12,13}. Himpunan kelipatan 3 yang terdapat di P adalah… A. {9} B. {3,9} C. {3,9,12} D. {3,6,9,12} Pembahasan Himpunan adalah kumpulan atau kelompok benda (objek) yang telah terdefinisi dengan jelas. Dari soal di atas, himpunan kelipatan 3 yang terdapat di P adalah {3,9,12}. Jawabannya : C |
Contoh Soal 5
| Jika A = {0,1} maka n(A) =… A. 0 B. 1 C. 2 D. 3 Pembahasan : n(A) adalah simbol dari kardinalitas atau banyaknya anggota suatu himpunan. Jadi banyaknya anggota suatu himpunan dari himpunan A adalah 2, yaitu 0 dan 1 Jawabannya : A |
Contoh Soal 6
| Diketahui M = {a, i, u, e, o} dan N = {a, u, o}, maka n(M ∪ N) adalah …. A. 5 B. 6 C. 7 D. 8 Pembahasan : – M = {a, i, u, e, o} – N = {a, u, o} M ∪ N = {a, i, u , e, o} Maka, n(M ∪ N) = 5 Jawabannya : A |
Contoh Soal 7
| Diketahui X = {x | x < 6, x є bilangan asli) dan Y = {x | – 1 ≤ x ≤ 5, x є bilangan bulat}, maka anggota (X ∩ Y) adalah …. A. {0, 1, 2, 3, 4, 5} B. {1, 2, 3, 4, 5} C. {-1, 0, 1, 2, 3, 4} D. {-1, 0, 1, 2, 3, 4, 5} Pembahasan : X = {x | x < 6, x є bilangan asli) = {1, 2, 3, 4, 5} Y = {x | – 1 ≤ x ≤ 5, x є bilangan bulat} = {-1, 0, 1, 2, 3, 4, 5} (X ∩ Y) = {1, 2, 3, 4, 5} Jawabannya : B |
Contoh Soal 8
| Jika n(A)= 10, n(B)= 8, dan n(A ∩ B)= 8, maka nilai n(A ∪ B) adalah …. A. 8 B. 9 C. 10 D. 11 Pembahasan : n(A)= 10, n(B)= 8, dan n(A ∩ B)= 8 n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 10 + 8 – 8 = 10 Jawaban: C |
Contoh Soal 9
Perhatikan diagram Venn berikut !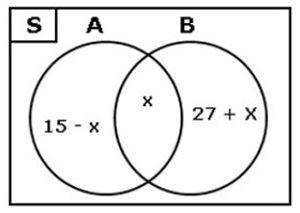 Jika diketahui n(S) = 50, n(A) = (15 – x), n(B) = (27 + x), maka banyaknya irisan A dan B adalah …. A. 5 B. 6 C. 7 D. 8 Pembahasan : n(S) = n(A) – x + n(A ∩ B) + n(B) + x 50 = 15 – x + x + 27 + x 50 = 42 + x 8 = x Jawabannya : D |
Contoh Soal 10
| Jika n(P) = 100, n(Q) = 120, dan n(P ∩ Q)= 80, maka n(P ∪ Q) adalah …. A. 80 B. 100 C. 120 D. 140 Pembahasan : n(P)= 100, n(Q)= 120, dan n(P ∩ Q)= 80 n(A ∪ B) = n(P) + n(Q) – n(P ∩ Q) = 100 + 120 – 80 = 140 Jawabannya : D |
Download Contoh Soal Himpunan Kelas 7 PDF
Adapun untuk mendapatkan contoh soal himpunan kelas 7 lebih lengkap lagi, maka berikut ini akan kami bagikan contoh soal yang bisa kalian download secara gratis.
File contoh soal kelas 7 ini berupa file PDF dan DOC untuk didownload tanpa melewati link-link membosankan. Cukup tekan unduh, maka contoh soal langsung terdownload.
Nah, itulah informasi dari inspired2write.com terkait contoh soal himpunan kelas 7 lengkap dengan materi serta kunci jawabannya. Dengan informasi contoh soal di atas, maka diharapkan bagi siswa kelas 7, mampu memahami soal himpunan.
Sedangkan untuk contoh-contoh soal matematika kelas 7 lainnya, mungkin kalian bisa mempelajari CONTOH SOAL PERSAMAAN LOGARITMA, untuk menambah keahlian di bidang matematika. Demikianlah informasi dari kami, semoga contoh soal kelas 7 di atas bermanfaat.