Contoh Soal Aljabar Kelas 7 – Aljabar merupakan salah satu materi SMP kelas 7 yang wajib kalian pelajari dan ketahui. Aljabar sendiri banyak dijumpai dalam kehidupan sehari-hari.
Sebagai contohnya, proses penjumlahan, perkalian, pengurangan serta pembagian merupakan bagian dari aljabar. Aljabar seringkali muncul dalam latihan soal Matematika kelas 7.
Salah satu metode belajar yang paling efektif untuk memahami materi aljabar yaitu dengan mempelajari contoh soal. Ini bisa kalian terapkan untuk mempersiapkan diri sebelum ujian.
Oleh sebab itu, dalam hal membantu kalian mempersiapkan diri sebelum ulangan Metematika. Berikut ini inspired2write akan menyajikan contoh soal aljabar kelas 7 SMP terbaru.
Pengertian Aljabar
Sebelum lanjut ke contoh soal aljabar kelas 7 SMP beserta pembahasannya. Sebagai pembukaan ada baiknya kalian memahami pengertian aljabar pada materi Matamatika terlebih dahulu.
Aljabar adalah cabang matematika yang mempelajari struktur, hubungan serta kuantitas. Untuk mempelajari hal-hal dalam aljabar digunakan simbol untuk merepresentasikan bilangan secara umum sebagai sarana penyederhanaan dan alat bantu memecahkan masalah.
Sebagai contoh, x mewakili bilangan yang diketahui, sedangkan y bilangan yang ingin diketahui. Bagian-bagian aljabar meliputi penjumlahan, pengurangan, perkalian dan pembagian.
Operasi Hitung Aljabar

Untuk menentukan perhitungan aljabar maka harus menggunakan operasi hitung aljabar. Adapun operasi hitung pada aljabar yang wajib diketahui yaitu sebagai berikut ini.
1. Penjumlahan dan Pengurangan Bentuk Aljabar
Pada bentuk aljabar, operasi penjumlahan dan pengurangan hanya bisa dilakukan pada suku-suku sejenis. Lebih jelasnya, simak contoh penjumlahan & pengurangan di bawah ini.
1x + 3x = 4x (bisa dijumlah karena sejenis)
5x – 2y = … (tidak bisa dikurangi karena tidak sejenis).
2. Perkalian Aljabar
Perlu diketahui, bahwasanya pada perkalian bilangan bulat berlaku sifat distribusi perkalian terhadap penjumlahan, yakni a × (b + c) = (a × b) + (a × c), serta perkalian terhadap pengurangan a × (b – c) = (a × b) – (a × c), untuk setiap bilangan bulat a, b, dan c.
3. Perpangkatan Aljabar
Operasi perpangkatan diartikan sebagai perkalian berulang dengan bilangan sama. Pada perpangkatan aljabar suku dua, koefisien tiap suku ditentukan menurut segitiga Pascal.
Contohnya, akan menentukan pola koefisien pada penjabaran bentuk aljabar suku dua (a + b)n, dalam hal ini n bilangan asli. Lebih jelasnya perhatikan penjelasan berikut ini :
(a+b)n = a + b → koefisiensinya 1 1
(a + b)³ = a + b (a + b)²
Dimana (a + b)² = (a + b) (a + b) = a² + ab + ab + b²
= a² + 2ab + b² = (a + b)³ = a + ba + b² = a + ba + 2ab + b²
= a³ + 2a²b + ab² + a²b + 2ab² + b² = a³ + 3a²b
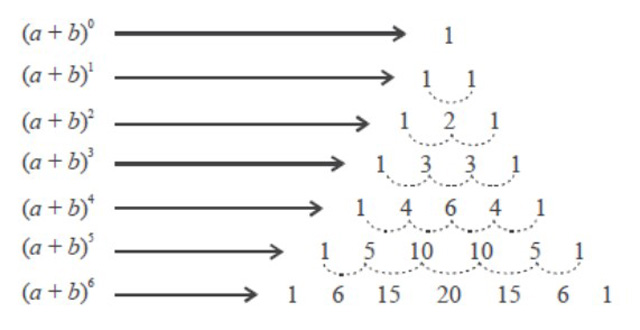
Pada segitiga Pascal di atas, bilangan di bagian bawahnya diperoleh dari penjumlahan bilangan yang berdekatan di bagian atasnya.
4. Pembagian Aljabar
Pembagian aljabar bisa kalian dapatkan dengan menentukan terlebih dahulu faktor sekutu masing-masing aljabar tersebut. Lalu melakukan pembagian pada pembilang & penyebutnya.
5. Substitusi pada Bentuk Aljabar
Substitusi pada bentuk aljabar maksudnya ialah nilai suatu aljabar bisa ditentukan dengan cara mensubstitusikan sembarang bilangan pada variabel-variabel bentuk aljabar terkait.
6. Menentukan KPK dan FPB Bentuk Aljabar
KPK serta FPB juga berlaku pada aljabar. Dimana untuk menentukan KPK dan FPB dari bentuk aljabar dilakukan dengan menyatakan bentuk-bentuk aljabar menjadi perkalian faktor primanya.
Contoh :
Tentukan KPK & FPB bentuk aljabar di bawah ini.
a. 12pq & 8pq
b. 45x2y3 & 50x4y3
Pembahasannya :
a. 12pq & 8pq
→ 12pq = 22 × 3 × p × q
→ 8pq = 32 × p × q2
→ KPK = 23 × 3 × pq2
→ KPK = 24pq3
b. 45x2y3 & 50x4y3
→ 45x2y3 = 32 × 5 × x3 × y2
→ 50x4y3 = 2 × 52 × x4 × y3
→ KPK = 2 × 32 × 52 × x5 × y3 = 450x5y3
→ FPB = 5 × x4 × y2 = 5x3y2
Contoh Soal Aljabar Kelas 7

Setelah memahami sekilas materi aljabar kelas 7. Adapun untuk contoh soal beserta dengan kunci jawaban serta pembahasannya, silahkan simak langsung pada ulasan di bawah ini.
A. Contoh Soal Aljabar Kelas 7 Pilihan Ganda
Contoh Soal 1
| Hasil penjumlahan dari -3a –6b + 7 dan 13a – (-2b) + 4 adalah …. A. 16a -8b + 11 B. 10a + 4b + 11 C. 10a -4b + 11 D. -16a -4b + 11 Jawabannya : C Pembahasannya : (-3a –6b + 7) + (13a – (-2b) + 4) = (- 3a + 13a) + (-6b + 2b) + (7 + 4) = 10a – 4b + 11 |
Contoh Soal 2
| Diketahui bentuk aljabar 3a2-7a -9, suku yang merupakan konstanta saja adalah…. A. 3a2 B. a C. -7 D. -9 Jawabannya : D Pembahasannya : Konstanta adalah bilangan yang tidak dimuati variabel. Jadi, konstanta dari bentuk 3a2-7a -9 adalah -9. |
Contoh Soal 3
| 8p + 5q dikurangkan dengan 2p – 4q maka hasilnya adalah …. A. 6p – q B. 6p + 9q C. -6p + q D. -6p – 9q Jawaban : B Pembahasannya : (8p + 5q)-(2p – 4q) = (8p – 2p) + (5q + 4q) = 6p + 9q |
Contoh Soal 4
| Hasil perkalian dari (4x – 5)(3x + 3) adalah …. A. 12x2-3x – 15 B. 12x2 +3x – 15 C. 12x2-27x – 15 D. 12x2 + 27x + 15 Jawaban : A Pembahasannya : (4x – 5)(3x + 3) = 12x2 + 12x – 15x – 15 = 12x2 – 3x – 15 |
Contoh Soal 5
| Bentuk -6x2 – x + 4y variabel-variabelnya adalah …. A. -6, -1 dan 4 B. x2, x dan y C. x + y D. x2 – 4y Jawaban : B Pembahasannya : Variabel adalah huruf yang ada pada suatu persamaan. Jadi, variabel dari -6x2 – x + 4y adalah x2, x & y. |
Contoh Soal 6
| Pada bentuk aljabar x2 – 2x – 5 koefisien-koefisiennya adalah …. A. x2 B. -2 C. – 2x dan – 5 D. -2 dan -5 Jawabannya : B Pembahasan : Koefisien adalah angka didepan variabel. Jadi, koefisien dari x2 – 2x – 5 adalah -2. |
Contoh Soal 7
| KPK dan FPB dari 6a2 & 8ab berturut-turut adalah …. A. 48 a2b dan 2a B. 24 a2b dan 4ab C. 24 a2b dan 2a D. 24 a2b dan 2ab Jawaban : C Pembahasan : 6a2 = 2 × 3 × a2 8ab = 23 × a × b KPK dari 6a2 & 8ab = 24 a2b = 23. 3 . a2. b FPB dari 6a2 & 8ab = 2a = 2 . a |
Contoh Soal 8
| Hasil pengerjaan dari (4c + 8d – 3e) – (6c + 2d – 2e) adalah …. A. -2c + 6d + e B. -2c + 6d – e C. -2c + 10d + e D. -2c + 10d – e Jawaban : B Pembahasannya : (4c + 8d – 3e) – (6c + 2d – 2e) = (4c-6c)+(8d-2d)-(3e+2e) = -2c + 6d – e |
Contoh Soal 9
| Jika a = 3, b = 0, c = -3 maka nilai dari [ax(b + c – a)] x (b + c) adalah …. A. 24 B. 9 C. 0 D. -18 Jawabannya : A Pembahasannya : [ax(b + c – a)] × (b + c) = [3x(0 + (-3) – 3)] × (0 + (-3)) = [3 x (-6)] × (-3) = (-18) × (-3) = 24 |
Contoh Soal 10
| Jika a = -3 , b =2 & c = -4, maka nilai dari 2a + 4b – 3c adalah …. A. 12 B. 13 C. 14 D. 15 Jawabannya : C Pembahasan : 2a + 4b – 3c = 2(-3) + 4(2) – 3(-4) = – 6 + 8 – (-12) = -6 + 8 + 12 = 14 |
B. Contoh Soal Aljabar Kelas 7 Esai
Contoh Soal 1
| Selesaikan bentuk aljabar berikut ini (3x – 2y) – (x – 3y) Pembahasan : (3x – 2y) – (x – 3y) = 3x – 2y – x – 3y = (3 – 1) x + (-2 – 3)y = 3x – x – 2y – 3y = 2x + (-5)y = 2x – 5y |
Contoh Soal 2
| Tentukan hasil dari (4p2 – 10p – 5) – (8p2 + 10p + 15) Pembahasan : (4p2 – 10p – 5) – (8p2 + 10p + 15) = 4p2 – 8p2 – 10p –10p – 5 – 15 = –4p2 – 20p – 20 |
Contoh Soal 3
| Bentuk paling sederhana dari 4(2x – 5y) – 5(x + 3y) Pembahasannya : 4(2x – 5y) – 5(x + 3y) = 4(2x – 5y) – 5(x + 3y) = 8x – 20y – 5x – 15y = 3x – 35y |
Contoh Soal 4
| Jika P = 4x2 + 3x & Q = 5x – x2 , maka tentukan nilai dari P – 2Q! Pembahasannya : P – 2Q = 4x2 + 3x – 2(5x – x2) = 4x2 + 3x – 10x + 2x2 = 4x2 + 2x2+ 3x – 10x = 6x2 – 7x |
Contoh Soal 5
| Bentuk sederhana dari 4(p – 3q) – 3(5q + 4p) adalah? Pembahasannya : 4(p – 3q) – 3(5q + 4p) = 4p – 12q – 15q – 12p = 4p – 12p –12q – 15q = – 8p – 27q |
Download Soal Aljabar Kelas 7

Setelah menyajikan beberapa contoh soal aljabar kelas 7 di atas, untuk mendapatkan contoh soal lebih lengkap lainnya maka bagi kalian siswa SMP/MTs kelas 7 bisa download di bawah ini.
Dimana download contoh soal di bawah ini disertai dengan soal latihan aljabar kelas 7. Kalian bisa mendownload contoh soal serta latihan soal aljabar kelas 7 secara gratis lewat link di bawah.
Nah, itulah informasi dari inspired2write.com terkait contoh soal aljabar kelas 7 beserta pembahasannya. Memahami dan mempelajari ilmu matematika terkait aljabar sangat penting.
Hal itu bisa kalian lakukan dengan mempelajari contoh soal aljabar, seperti halnya mempelajari CONTOH SOAL HIMPUNAN KELAS 7 agar lebih menguasai materi terkait himpunan. Demikianlah informasi contoh soal dari kami, semoga contoh soal di atas bermanfaat.